프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
문제 설명
철호는 수열을 가지고 놀기 좋아합니다. 어느 날 철호는 어떤 자연수로 이루어진 원형 수열의 연속하는 부분 수열의 합으로 만들 수 있는 수가 모두 몇 가지인지 알아보고 싶어졌습니다. 원형 수열이란 일반적인 수열에서 처음과 끝이 연결된 형태의 수열을 말합니다. 예를 들어 수열 [7, 9, 1, 1, 4] 로 원형 수열을 만들면 다음과 같습니다.
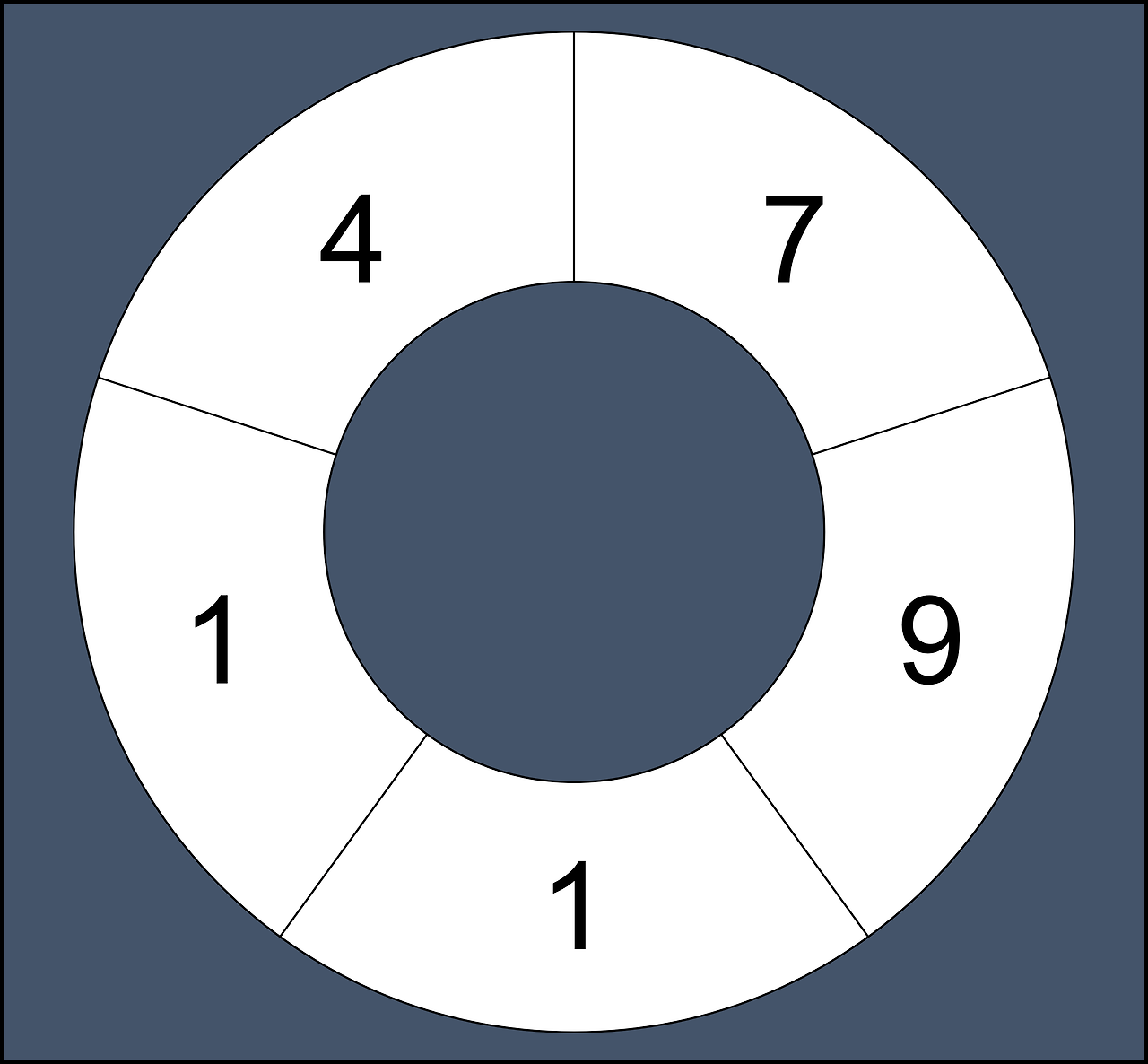
원형 수열은 처음과 끝이 연결되어 끊기는 부분이 없기 때문에 연속하는 부분 수열도 일반적인 수열보다 많아집니다.원형 수열의 모든 원소 elements가 순서대로 주어질 때, 원형 수열의 연속 부분 수열 합으로 만들 수 있는 수의 개수를 return 하도록 solution 함수를 완성해주세요.
제한사항
- 3 ≤ elements의 길이 ≤ 1,000
- 1 ≤ elements의 원소 ≤ 1,000
입출력 예
| elements | result |
| [7, 9, 1, 1, 4] | 18 |
입출력 예 설명
입출력 예 #1
길이가 1인 연속 부분 수열로부터 [1, 4, 7, 9] 네 가지의 합이 나올 수 있습니다.
길이가 2인 연속 부분 수열로부터 [2, 5, 10, 11, 16] 다섯 가지의 합이 나올 수 있습니다.
길이가 3인 연속 부분 수열로부터 [6, 11, 12, 17, 20] 다섯 가지의 합이 나올 수 있습니다.
길이가 4인 연속 부분 수열로부터 [13, 15, 18, 21] 네 가지의 합이 나올 수 있습니다.
길이가 5인 연속 부분 수열로부터 [22] 한 가지의 합이 나올 수 있습니다.
이들 중 중복되는 값을 제외하면 다음과 같은 18가지의 수들을 얻습니다.
[1, 2, 4, 5, 6, 7, 9, 10, 11, 12, 13, 15, 16, 17, 18, 20, 21, 22]
✅ 정답 코드 (슬라이딩 윈도우 알고리즘)

슬라이딩 윈도우 알고리즘을 활용해 해결하였다.
- 연속 부분 수열의 길이를 i로 두고, 길이가 1인 연속 부분 수열, 길이가 2인 연속 부분수열 ... 경우의 수를 모두 탐색한다.
- 초기 합 7+9+1을 먼저 결과 배열에 추가한 후,
- for문으로 left와 right를 한 칸 증가시켜가며 sum값을 구한다.
- 이전 합(7+9+1)에서 left값(7)은 빼고, 새로 들어온 right값(1)은 더하면서 계속 새로운 sum을 구한다.
- sum을 결과 set에 넣는다. set을 사용함으로서 중복되지 않는 것의 개수만 카운트한다.
def solution(elements):
n = len(elements)
result = set() # set으로 중복되지 않는 것의 개수만 카운트
for i in range(1, n+1):
left = 0
right = i-1
sum = 0
# 초기 합 구하기
for j in range(i):
sum += elements[j]
result.add(sum) # 초기 합을 결과 배열에 추가
# 슬라이딩 윈도우
for j in range(1, n):
right = (right+1) % n
sum = sum - elements[left] + elements[right]
left = (left + 1) % n
result.add(sum)
return len(result)
- % n 은 원형 수열이기 때문에 인덱스 초과를 막기 위해 나머지 값을 활용
- left과 right값을 하나씩 옮겨주면서 sum값에 elements[left]는 빼고, elements[right]는 더함
❎ 시간초과 3중 for문 풀이

슬라이딩 윈도우 알고리즘을 생각하기 전에는 3중 for문을 이용해서 브루트포스 알고리즘으로 가능한 sum을 다 구해보는 방법을 시도했다.
- [첫 번째 for문] 연속 부분 수열의 길이를 i로 두고, 길이가 1인 연속 부분 수열, 길이가 2인 연속 부분수열 ... 경우의 수를 모두 탐색한다.
- [두 번째 for문] j 값을 바꿔가며 수열의 시작 위치를 조정한다
- [세 번째 for문] k 값으로 수열의 길이에 맞게 각 값을 더해가며 sum을 구해서 결과 set에 추가한다. (중복을 제거하기 위해 list가 아닌 set 이용)
def solution(elements):
n = len(elements)
result = set()
for i in range(1, n+1):
for j in range(n):
sum = 0
for k in range(j, j+i):
sum += elements[k%n]
result.add(sum)
return len(result)

로직은 맞는 것 같았지만 for문을 세 개나 사용했다보니, 시간복잡도 문제로 몇 개의 테스트케이스에서 시간초과가 발생했고, 슬라이딩 윈도우를 활용해 마지막 sum을 구하는 부분의 for문을 없애서 2중 for문으로 바꾸었더니 해결되었다!
슬라이딩 윈도우 (Sliding Window)
- 고정 사이즈의 윈도우가 이동하면서 윈도우 내에 있는 데이터를 이용해 문제를 풀이하는 알고리즘
- 배열이나 리스트의 요소의 일정 번위의 값을 비교할 때 사용하면 매우 유용하다.

0부터 n까지의 배열에서 최대의 합을 찾으려면, 위 그림과 같이 0~2번쨰 합을 먼저 구해놓은 뒤,
- 이전 합에서 0번째 수(left) 는 빼주고, 4번째 수(right) 는 더하면 다음 합을 구할 수 있고,
- 이전 합에서 1번째 수(left) 는 빼주고, 5번째 수(right)는 더하면 다음 합을 구할 수 있다.
1차원 배열을 2회 이상 반복적으로 탐색해야 할 경우 O(n^2) 이상이 걸릴 시간 복잡도를, 부분 배열을 활용하여 O(n)으로 줄일 수 있는 장점이 있다.
📌 참고 링크
슬라이딩 윈도우 테크닉
: 주어진 배열에서 고정 크기의 윈도우(창문)를 이동하면서, 윈도우 내의 정보를 처리하는 알고리즘 기법배열이나 리스트와 같이 순차적인 자료구조에서 연속적인 구간을 처리해야할 때 유용하
velog.io
[Algorithm] 슬라이딩 윈도우(Sliding Window) 알고리즘 with Java
알고리즘에 대한 이해 !'슬라이딩 윈도우'란 ?슬라이딩 윈도우라는 말은 옆으로 '한칸씩 슬라이딩한다 .'라는 말과 배열의 그림이 창문을 모아놓은 것 같아 슬라이딩 윈도우라는 명칭이 되었다
chanhan.tistory.com
'개발공부 > 코테' 카테고리의 다른 글
| [백준 2960: 도영이가 만든 맛있는 음식] 파이썬 풀이 _ 조합 내장 함수 combinations (1) | 2024.07.08 |
|---|---|
| [백준 2885: 초콜릿 식사] 파이썬 풀이 (1) | 2024.07.05 |
| [백준 10773: 제로] 파이썬 풀이 _ 스택 (stack) (0) | 2024.02.01 |
| [백준 7785: 회사에 있는 사람] 파이썬 풀이 _ list와 set의 시간복잡도 (0) | 2024.01.22 |
| [백준 10809: 알파벳 찾기] 파이썬 풀이 (1) | 2023.11.28 |



